Compression Spring Design
Compression Spring Design
Definition:
kum'prê[sh]un spri[ng] A compression spring is a mechanical device in the shape of a helix made from spring wire. It is used to store or release energy. It can also absorb shock or maintain a force between two surfaces.
Overview:
Compression springs are coil springs that resist a compressive force applied axially. Compression springs or coil springs have a spring constant and may be cylindrical springs, conical springs, tapered , concave or convex in shape. Compression springs are linear and thus have the same rate per inch throughout the entire spring. You can have large compression springs, heavy duty compression springs, conical compression spring, small compression springs, or even micro compression springs. Coil compression springs are wound in a helix usually out of round wire. The changing of compression spring ends, direction of the helix, material, and finish all allow a compression spring to meet a wide variety of special industrial needs. Coil springs can be manufactured to very tight tolerances, this allows the coil spring to precisely fit in a hole or around a shaft. A digital load tester, or coil spring compression tester can be used to accurately measure the specific load points in your metal spring. The possibilities are almost endless because there are so many applications for metal springs.
Compression Spring Applications:
Compression springs can accomplish many types of applications such as pushing or twisting, thus allowing you to achieve numerous results. Compression springs offer resistance to linear compressing forces (push) and are in fact one of the most efficient energy storage devices available. A ballpoint pen is an excellent example of how small compression springs work. The small spring will compress when the pen is clicked and then the small spring will return to it's original position. Other uses include vibration dampening and high temperature applications.
Compression springs that are engineered for high temperature applications can reach up to 1,100 degrees Fahrenheit.
Ends:
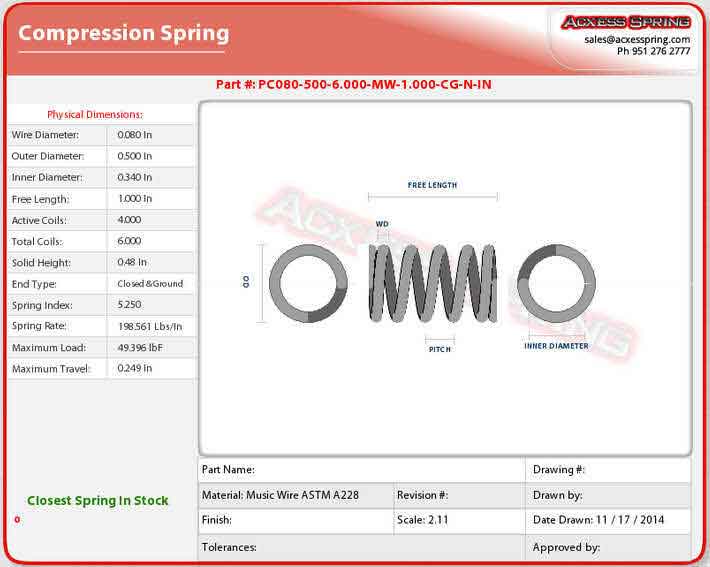
Compression spring ends are usually closed and square. These ends can also be closed and ground, or have open ends. Furthermore a compression spring can have hooks on one end or both ends so as to fasten it to your particular assembly. The ends of compression spring can also be close wound for a certain number of coils on the ends permitting the spring to remain in a vertical position. The squareness influences how the axis force produced by the spring can be transferred to adjacent parts. Another application includes being able to thread a closed end coil spring onto a threaded shaft for fastening purposes. Other end configuration examples are reduced end diameters like a barrel spring on a bicycle seat. Springs can have dual diameters as well as triple diameters for achieving different assembly situations.
General Step By Step For Designing A Compression Spring
1. Know where your spring is going. Does it need to fit over a shaft, thus the inner diameter is a fixed measurement. Does it need to go in a hole, thus the outer diameter is a fixed measurement. Does it need to fit into a space that is a certain depth or width, thus the spring would have a maximum free length.
2. What is the spring's environment. This is necessary because certain materials are best for certain designs. For example stainless steel is good for salt water or medical applications and Inconel is best for springs being used at very high temperatures.
3. You need to determine the purpose of the compression spring. Is is going to be pushing down a certain object, will it be sustaining any type of weight or stress?
4. Know how far your spring needs to travel to complete the task in number 3. You can calculate the maximum spring compression of your compression spring on our Free Online Maximum Spring Compression Calculator.
5. Consult a spring engineer you trust to help you achieve all of the steps above including designing your spring as economical and efficient as possible.
For more helpful compression spring design tips visit: planetspring.com
End Configurations
Closed and Squared Ends

Closed and Squared Ends: Means that the last coil is closed. This is done so that the spring can stand on it's own.
Closed and Ground Ends

Closed and Ground Ends: means an additional grinding operation has to be applied to the closed end configuration. Grinding removes material from the spring's end coils to create a flat surface so the spring can stand up straight vertically.
Open Ends

Open Ends Ground Square: are ends that there is no reduction in pitch and the ends remain open.
Double Closed Ends

Double Closed Ends: are the last two coils on each end that are closed and have no pitch.
The Spring Force Chart
Use this chart to adjust your spring force accordingly
More Force (MF)
| Smaller OD = MF |
| Less Coils = MF |
| Thicker Wire = MF |
| More Travel = MF |
Less Force (LF)
| Larger OD = LF |
| More Coils = LF |
| Thinner Wire = LF |
| Less Travel = LF |
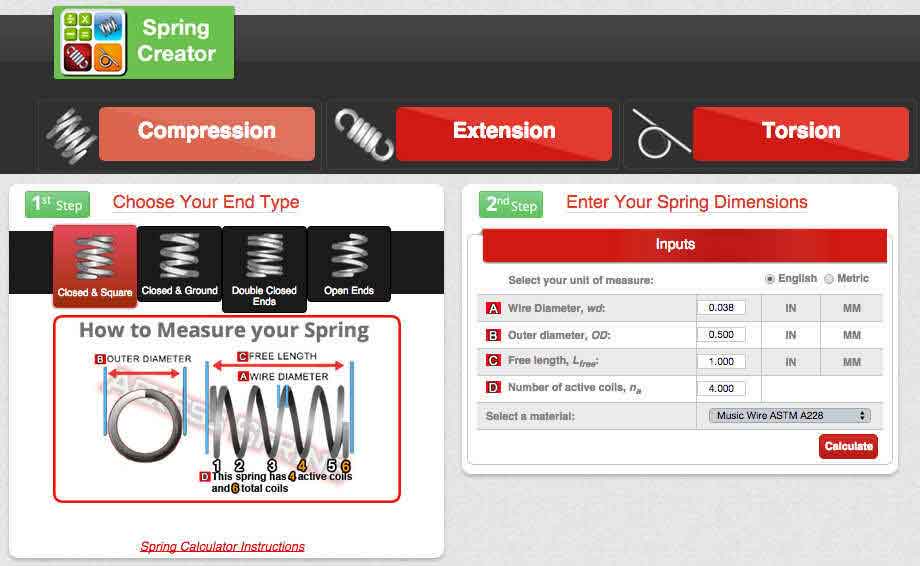
Key Parameters for Compression Spring Design
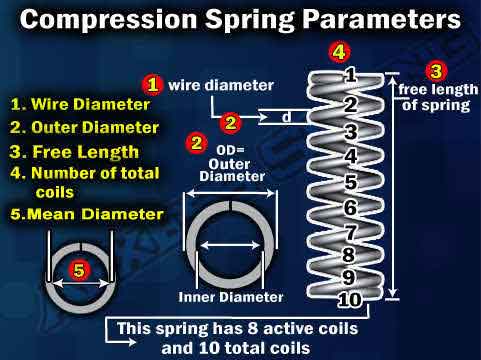
- Outside diameter:The outer diameter of a spring.
- Inner diameter: The Inner diameter of a spring.
- Wire diameter: The outer diameter of round wire.
- Free Length: The overall length of a spring in the unloaded position.
- Solid Height: The length of a compression spring when all the coils are fully compressed and touching.
- Spring Rate: (Stiffness) Is the spring rate of force in pounds per inch of compression. Examples: If the spring rate of a compression spring is 10 lbs. It will take you 10 lbs of force to move it 1 inch of distance. If you move it 2 inches of distance it will take you 20 lbs of force. The rate is linear.
Formulas for compression spring constant or rate:
k = Gd^4 / [8^3D na]G = E / 2(1 + V)
d = D outer - d
Variables Used In Compression Spring Rate Formula
- Spring Wire Diameter = d
- Spring Outside of Spring = D outer
- Mean Diameter Of Spring = D
- Young's Modulus of material = E
- Max force at Solid = f max
- shear modulus of material = G
- Free Length = L free
- Wire Length = L wire
- Solid Height = L solid
- Maximum load possible =L max
- Wahl correction factor = W
- Spring Constant = K
- Active Coils = na
- Total Coils = nt
- Density of Material = P
- Poisson ratio off Material = V
- Rise angle of spring coils = 0
- Maximum sheer stress = T max




 Español
Español