Linear Spring Design
Definition: The process of building a design for a linear coil spring made from helically wound round wire.
Linear springs are helical springs with a linear constant force. This means that it’ll take a proportional amount of load for the spring to deflect a certain distance of travel. Linear springs are compression springs and extension springs. What differs these types of springs from a torsion spring, is that torsion springs exert a radial force. Compression and extension springs exert a constant amount of force per every inch or millimeter of distance traveled (fraction of an inch or millimeter as well). The amount of load it’ll take a spring to travel a required distance depends on the spring constant, also known as spring rate or spring force. The difference between a linear compression spring and a linear extension spring is not only the differences in their physical form or how one is used to compress (be pushed on) while the other is used to extend (be pulled on). The difference is that the working loads on a compression spring are only based on spring rate while the constant forces for an extension spring are also based on initial tension.
Linear Compression Springs
Compression springs deflect in a straight line, whether it might be vertical or horizontal. The amount of force they exert is based on physical dimensions like the wire diameter, outer diameter, free length, active coils (space in between active coils), and the material type used. Some springs may be very similar in shape or size but the force they exert and their elasticity depends on the proportion of all of the dimensions that make up the linear spring. This is due to stress factors like spring index or the proportion within the amount of coils (or space in between these coils) and the free length. If your spring has a tight index (a large wire diameter in proportion to the outer diameter), it is going to be under stress so it will be able to carry a significant load but might not be able to travel (or deflect) much. The same goes for when your spring has a long free length with very few coils. The opposite of these given examples (large index or many coils in proportion to the free length) gives you the opposite reaction because it’ll be under less stress: the spring will be able to deflect much more but it will not be very strong. The following formulas and examples will demonstrate how this works.

Spring Index
(This formula works for both compression and extension springs)
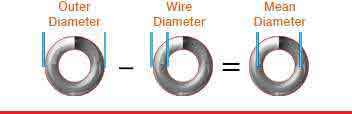
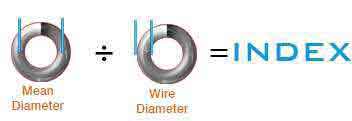
Spring index is the proportional ratio between your spring’s diameter and its wire diameter. To calculate spring index, you must subtract one wire diameter from the outer diameter. The result is what we call the mean diameter as shown in the diagrams. Then, you must divide the mean diameter by the wire diameter. The outcome of this calculation is your spring’s index. A 4:1 index is too tight while a 15:1 index is too loose so you want to make sure that you’re somewhere in between.
Formula for Spring Index:
Index = (Outer Diameter – Wire Diameter) ÷ Wire DiameterI = (OD – WD) ÷ WD
Example: You have an outer diameter of 0.5” and a wire diameter of 0.05”.
I = (0.5 – 0.05) ÷ 0.05I = 0.45 ÷ 0.05
I = 9

Spring Rate
Spring rate derives from your spring’s working loads. Knowing the two values that make up your spring’s working loads will help you calculate how strong your spring needs to be in order to meet those working loads.
Formula for Spring Rate:
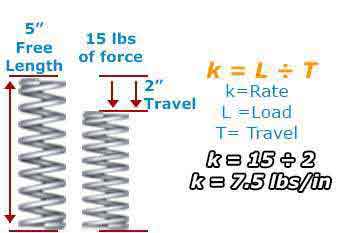
Rate = Load ÷ Travelk = L ÷ T
Example: Your spring should travel 2” under a 15 lb. load.
k = 15 ÷ 2k = 7.5
Linear Extension Springs
Extension springs also deflect in a straight line. Based on their physical dimensions, the amount of load being placed on the spring is proportional to the spring travel because these springs exert a constant force. Linear extension springs have another value that must be taken into note when doing load calculations. This value is known as initial tension. Initial tension is the gathered energy already gathered in between your extension spring’s coils thus keeping the coils tightly together. It is released once your extension spring is pulled enough to where you are able to see light in between its coils. This is an additional load which must be added to the load you calculated using only the spring rate. To calculate load you must multiply the spring travel by the spring rate. This will tell you how much load you need in order to meet your required extended length. Once you have calculated that value, you must add the initial tension to the load. The result of this calculation will be the total load it’ll take your spring to travel the distance it is required. The force and elasticity will also depend on the physical dimensions. Follow the index formula provided for compression springs to make sure your spring isn’t under a lot of stress.
Spring Load
Spring load for extension springs will usually be larger than one thinks due to the fact that most people use the formula previously provided for compression springs. That formula doesn’t include initial tension. This is why we have provided you with the corrected formula to calculate extension spring load.
Formula for Spring Load
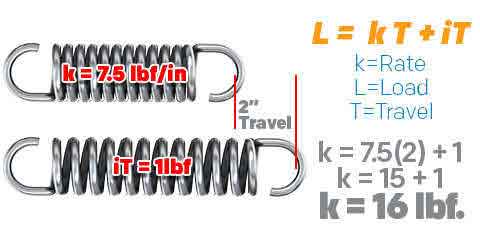
Load = Rate x Travel + Initial Tension
L = k T+ iT
Example: You have a spring with a spring rate of 7.5 lbf/in., initial tension of 1lbf., and a traveled distance of 2”.
L = 7.5 x 2 + 1L = 15 + 1
L = 16
Linear Extension Spring Load Formula




 Español
Español