Spring Constant Calculator
Spring constant is the amount of force required to move the spring a set amount of distance. The set amount of distance is determined by your units of measurement and your spring type.
For example if you are calculating the spring constant of a compression spring using English measurements your value would be pounds of force per inch of distance traveled. If you are using the metric system your spring constant would be in Newtons per millimeter of distance traveled. Extension springs have the same units of measurements as compression springs, however torsion spring constant is calculated in force per 360 degrees of travel.
Compression Spring Constant
When determining a spring constant there are 2 different formulas you can use depending which information you have available to you. The first formula is the one most commonly used when you know the dimensions on your spring but do not know your load and distance traveled on the spring.
Compression Spring Constant Formula
k = Gd^4 / 8D^3N
Explanation of Symbols:
- d = wire size (inches)
- D = Mean Diameter (inches)
- N = Number of active coils
- D / d = Index correction
- G = Shear Modulus of Material
- k = Spring Constant
G-Value for Common Spring Materials
- Music Wire = 11.5 x 10^6
- Stainless Steel = 11.2 x 10^6
- Phospher Bronze = 5.9 x 10^6
- Monel = 9.6 x 10^6
- Inconel = 11.5 x 10^6
- Copper = 6.5 x 10^6
- Beryllium Copper = 6.9 x 10^6

Example of Calculating the Compression Spring Constant
- d = 0.035 inches
- OD = 0.500 inches
- D = 0.465 inches
- N = 8
- Wire Type = Music Wire
- G = 11.5 x 10^6 psi
- FL = 1.000 inches
k = (11.5 x 10^6) (0.035)^4) / 8 (0.465)^3 (8)
k = 17.2571875 / 6.434856
k = 2.68 lbs / inch
Calculate a Required Spring Constant
The other way to calculate the compression spring constant on your spring is if you know the load you want to achieve at a certain distance traveled. The formula to figure out your spring constant from a known load and distance traveled is:
Rate = Load / Distance TraveledFor Example:
- Load = 10 pounds
- Travel = 4 inches Rate = 10 lbs / 4 inches
Rate = 2.5 pounds / inch
Extension Spring Constant
Calculating your extension spring constant uses the same formula as the compression spring constant calculation. Make sure when measure your extension spring you have the correct measurement for each value. For more information on this please visit our spring measurement and specifications page.
Extension Spring Constant Formula
k = Gd^4 / 8D^3N
Explanation of Symbols:
- d = wire size (inches)
- D = Mean Diameter (inches)
- N = Number of active coils
- D / d = Index correction
- G = Shear Modulus of Material
- k = Spring Constant
G-Value for Common Spring Materials
- Music Wire = 11.5 x 10^6
- Stainless Steel = 11.2 x 10^6
- Phospher Bronze = 5.9 x 10^6
- Monel = 9.6 x 10^6
- Inconel = 11.5 x 10^6
- Copper = 6.5 x 10^6
- Beryllium Copper = 6.9 x 10^6
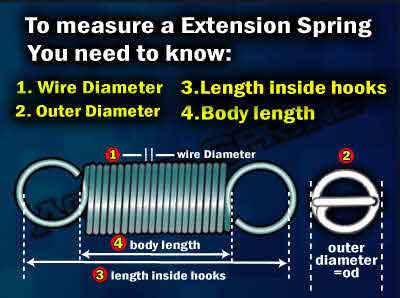
Example of Calculating the Extension Spring Constant
- d = 0.044 inches
- OD = 0.425 inches
- D = 0.381 inches
- N = 5
- Wire Type = Music Wire
- G = 11.5 x 10^6 psi
- FL = 1.250 inches
k = (11.5 x 10^6) (0.044)^4) / 8 (0.381)^3 (5)
k = 43.103104 / 2.21225364
k = 19.472 lbs / inch
Calculate a Required Spring Constant
The other way to calculate the extension spring constant on your spring is if you know the load you want to achieve at a certain distance traveled. The formula to figure out your spring constant from a known load and distance traveled is:
Rate = (Load – Initial Tension) ÷ Distance TraveledFor Example:
- Load = 10 pounds
- Initial Tension = 2.5 pounds
- Travel = 0.5 inches Rate = (10 lbs – 2.5 lbs) ÷ 0.5 inches
Rate = 14 pounds / inch
Torsion Spring Constant
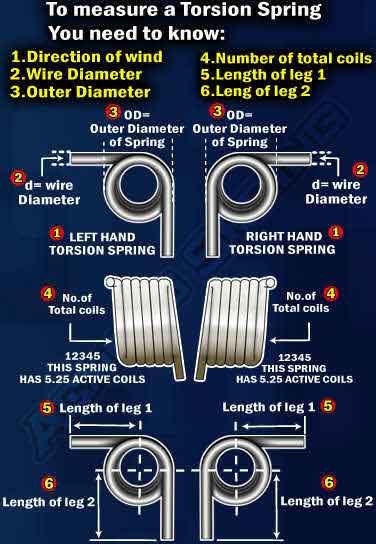
Calculating torsion spring constant is a little different than calculating the sspring constant for compression or extension springs. Since a torsion spring travels in degrees and not linearly it needs a different formula. Below you can see the formula for torsion spring constant and an example of how the formula works.
Rate per 360 Degrees
(R) = Ed^4 / 10.8 DN
Explanation of Symbols:
- d = wire size (inches)
- D = Mean Diameter (inches)
- N = Number of active coils
- D / d = Index correction
- G = Shear Modulus of Material
- k = Spring Constant
Modulus of Elasticity "E" for common spring wires.
PSI x 10^6
- Music Wire = 30 psi
- Stainless Steel = 28 psi
- Chrome Vanadium = 30 psi
- Chrome Silicon = 30 psi
- Phosphor Bronze = 15 psi
Torsion Spring Rate Calculation Example
Formula
Rate Per 360 degrees = Ed^4 / 10.8 DNSpring Parameters
- d = 0.035 inches
- OD = 0.500 inches
- D = 0.465 inches
- N = 3
- Wire Type = Music Wire
- E For Music Wire = 30 x 10^6
Example
Rate Per 360 Degrees = (30 x 10^6) (0.035^4) / 10.8 (0.465)(3)Rate Per 360 Degrees = 45.01875 / 15.066
k = 43.103104 / 2.21225364
Rate Per 360 Degrees = 2.988 pounds / 360 degrees
To determine your rate per degree divide the above answer by 360
Rate Per Degree = Rate Per 360 Degrees / 360Rate Per Degree = 2.988 / 360
Rate Per Degree = 0.0083 pounds / degree




 Español
Español


